私が目測するのは、目通り幹囲である。
　なぜ、自ら測定する気になったのか。また、なぜメジャーでの実測でなく、「目測」なのかを記してみたい。
　
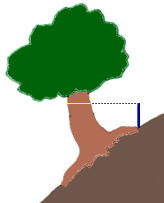
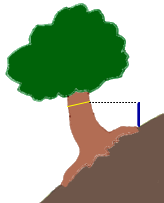
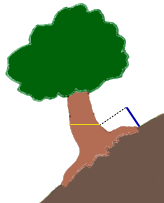
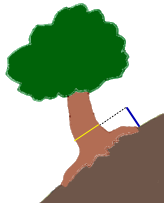
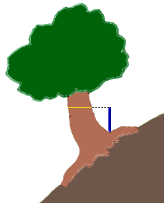
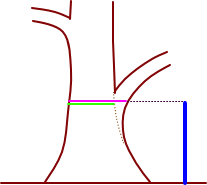
　旧環境庁が、平成元年（1989）３月にかけて実施した、いわゆる「緑の国勢調査」における「巨樹・巨木林調査実施要項」によれば、地上約１．３ｍの高さでの幹回りを「センチメートル単位で測定する」ことが指示されている。幹囲が１０ｍを超す巨樹も珍しくはないから、９９．９％以上の精度を要求したわけだ。
　センチメートルまで測ることで、巨樹に順位をつけ、人々の関心を喚起して、ひいては巨樹を保護する国民的なムードを醸成しようと意図したのだと思う。

　しかし、同一の個体であっても、さまざまな資料に掲載される値は、必ずしも一致していない。なかには１ｍ以上も異なっていることすらある。
　それぞれ専門家ともいえる人たちが真摯に測定しているのに、誤差が１０％以上もあるのはどういうことか。それは測定している部位が異なっていること以外には考えられない。

　地上１．３ｍとは、どこを指すのだろう。前掲の実施要項では、斜面上に立つ場合は山側で測ること、根上がりの個体では根の上部から測ること、の２点が指示されているほか、特別な指示はない。要は根際の地面から垂直に１．３ｍ高い点を求め、その点を含む水平面で立木を輪切りにした断面を考えているようだ。
　でも、実際に木を目の前にしたとき、迷ってしまう。水平面で輪切りにすることが、私たちの直感的な太さと、必ずしも一致しないからである。
　下のようなケースについて、あなたなら、fig.１～fig.８のどこを測定するべきだと思うだろうか。
fig.1 fig.2 fig.3 fig.4
fig.5 fig.6 fig.7 fig.8
　各地の巨木を、複数の測定者が測定してデータを求めるのであるから、測定方法を統一しておくことは当然である。その点で、なんら異論を唱えるものではないが、アマチュアの気楽さから勝手なことを言わせてもらえば、メジャーで厳密に測定しようとすればするほど、私たちの太さの実感からは離れてしまう約束事もあるようだ。
　
　たとえば、右図Ａ・Bのケースでは、どちらが太いように感じるだろうか。
　このように、幹断面に凹凸がある場合には、凹凸に沿ってメジャーをあてて測定することになっているらしい。（株立ちの木では幹の各々の幹周を合計するのであるから、それと整合性を持たせようとしたのだと思われる）
　しかし、そのため、私たちの直感とは異なり、AよりもBの方が幹回りの測定値は大きくなる。（※注）

　また、ちょうど１．３ｍの高さに枝が出ていたらどうしよう。メジャーで測定しようとしたならば、必然的に右図のピンク線のように測定せざるを得ない。私たちが直感的に感じる木の太さは緑線なのだが、これはメジャーでは測定できない。

　どうせアマチュアなら、詳しい測定は専門家に任せて、自分の直感で押し通そう。これが、私が目測を始めた一つの理由である。

※注）平成２０年の改訂版計測マニュアルでは、この点は改められたようだ。ほかにもさまざまなケースにおける測定の実例が示されており、その内容は一応納得できる。（この計測マニュアルは、環境省「巨樹・巨木林調査」のページからＰＤＦファイルで入手可）


　さて、本題の目測方法についてである。
　
方法１

>①まず木の回りを半周して、最も太く見える位置を見つける。（Ｐ）
②そこから木に向かって、まっすぐ近づけるだけ近づく。（Ｑ）
③直線ＰＱと直角をなす向きに１０歩あるく。（Ｒ）
④ＱＲと直角な向きに、木が正面に見えるまで移動する。（Ｓ）
⑤両手をいっぱいに伸ばし、手に持った３０ｃｍものさしで、目通りの径をミリメートルまで測る。（これがｂ）　
⑥次に、そこから木に向かってまっすぐ近づけるだけ近づく。（Ｔ）
⑦直線ＳＴと直角をなす向きに１０歩あるく。（Ｕ）
⑧ＴＵと直角な向きに、木が正面に見えるまで移動する。（Ｖ）
⑨ここでも両手をいっぱいに伸ばし、目通りの径を測定する。（これがａ）
　
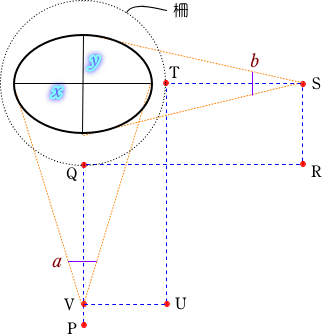
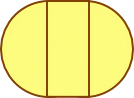
　測定は以上である。あとは自分の１０歩距離と、目からものさしまでの距離がわかれば、比例計算により長径 ｘ と短径 ｙ を計算することができる。
　かなりいい加減な測定方法のように思われがちだが、平地に立っている木の場合には、これで結構いい値が出る。
　１０歩距離も、慣れれば誤差はかなり小さくできるものである。因みに伊能忠敬の１０歩距離は６．９ｍだったらしい。（私は７．０ｍ±０．２ｍ）

　次の問題は、長径 ｘ と短径 ｙ から周長を計算するステップである。
　私は、下の３つの幹断面モデルに基づいて計算している。楕円断面モデルでは、簡単な計算式から周長を求めることはできないので、Visual Basic で数値計算プログラムを組んだ。
　しかし、既知のデータと比較してみると、大抵のケースで下図Ｂの「半円＋長方形＋半円」モデルが一番近い値となった。これならば周長は

　　　　　　　　　　　　　　　　（３．１４× ｙ）＋２（ｘ－ｙ）

であり、コンピュータ・プログラムに依らなくても求めることが出来る。
Ａ　楕円 Ｂ　半円＋長方形＋半円 Ｃ　半楕円＋半円
　木の周囲の土地に起伏があったり、あまりに広い範囲を柵で囲ってあったりすると、上記の方法で測定しても良い値は期待できない。そのような場合には、（道具が必要だが）次の「方法２」が便利である。
方法２

①まず、木の回りを半周して、最も太く見える位置を見つける。（Ｐ）
②測定器を用いて距離ＰＱを測定する。
③両手をいっぱいに伸ばし、目通りの径を、ものさしでミリメートルまで測定する。（これが ａ ）
④次にＯＰとＯＲが直角になるような位置Ｒを定める。
⑤距離ＲＳを測定する。
⑥上記③と同様に ｂ を測定する。
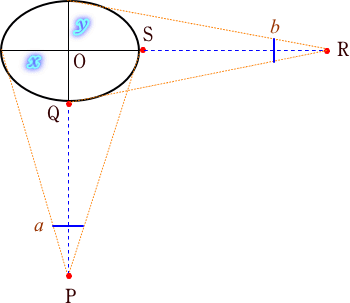
　両手をいっぱいに伸ばしたときの、目からものさしまでの距離を ｄ とすると、

　　　　　　　ｘ　：　ａ　　＝　　ＰＱ＋（ｙ／２）　：　ｄ
　　　　　　　ｙ　：　ｂ　　＝　　ＲＳ＋（ｘ／２）　：　ｄ

の２式が成り立つので、これらより ｘ，ｙ を求めることができる。
　このあとは「方法１」と同様に幹回りの長さを求めればよい。

　柵のため、Ｑ点やＳ点には近づけないことが前提だから、ＰＱやＲＳの長さを求めるには距離測定器が必要である。
　
　最初は、超音波を用いる装置を使ってみた。小型で廉価だったからである。
　しかし、この種の装置は、反射音が正確に戻ってくるような環境でないとうまく働かない。
　幹が斜上していたり、幹は直立しているのだが、斜面に立つために、測定器からの超音波が斜めに入射するようなケースでは、反射音がうまく戻ってこない。
　また、周囲に別の木があったり、低い枝が出ていたりすると、いったいどこで音波が反射してきたのか（どこまでの距離が測定されたのか）判明しない欠点がある。
　超音波の反射を用いた装置は、このような測定には適しないことがわかった。

　現在使っているのは、「レンジング」と名付けられた光学測定装置である。水平に離れた２つの窓から入る像が合致するように角度を調整し、その角度から距離を計算する仕組みだ。
　これは、周囲に様々な物体が錯綜していても、ピントが合った物体までの距離が測定されるのであるから、目標物がきちんと弁別できる利点がある。
　現時点では重宝して使っているが、欠点もある。薄暗いところでは測定しにくいこと、カタログ・データほどの高精度は、よほど条件が良くないと得られないことである。

　レーザー反射を用いた「ライトスピード」という魅力的な装置もあるが、現時点ではまだ近距離の測定には向かないようだ。時間計測のクロック周波数が今の２０倍ほどになって、測定誤差が１０ｃｍを切るようになったら、求めたいと思っている。
超音波距離測定器 レンジング
　少々面倒くさい内容になってしまったが、以上が「私の目測法」である。